다이나믹 프로그레밍
작은 문제가 큰 문제 안에 중첩되어 있는 경우에 작은 문제의 답을 다른 작은 문제에 이용함으로써 효율적으로 계산하는 방법이다. 벨만 기대방정식으로 푸는 것이 정책 이터레이션이고 벨만 최적 방정식으로 푸는 것이 가치 이터레이션이라고 한다.
정책 에터레이션
정책은 에이전트가 모든 상태에서 어떻게 행동할 지에 대한 정보이다. 처음에는 무작위로 행동을 정하는 정책으로 시작하여 아래의 그림처럼 무한히 반복하면 최적 정책으로 수렴된다.
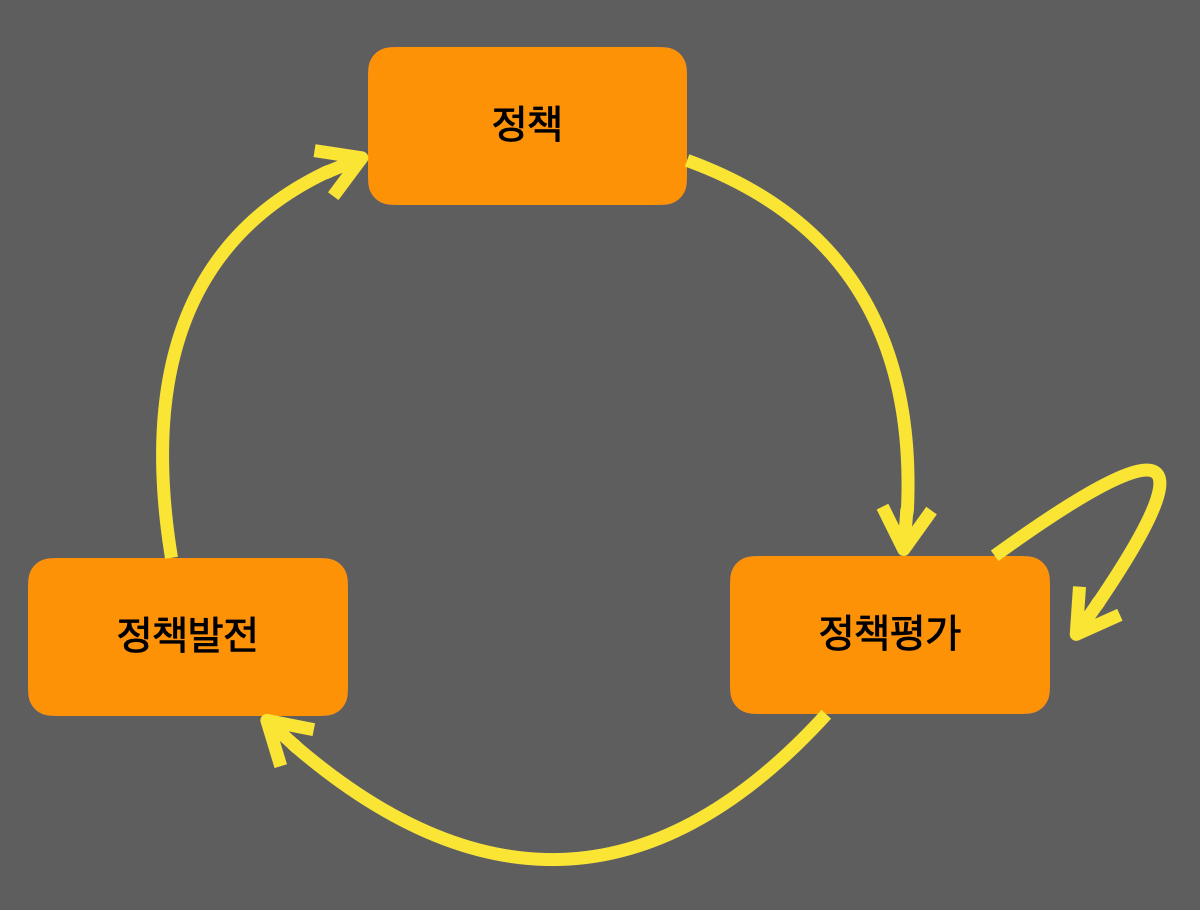
정책평가
가치함수를 통해서 정책을 판단한다. 현재 정책에 따라 받을 보상의 정보가 정책의 가치가 되어 평가를 할 수 있다.
$V_{\pi}(s)=E_{\pi}[R_{t}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots|S_{t}=s]$을 통해 가치함수를 구하기 위해서는 환경의 모든 정보를 알아야하지만 이는 불가능하다.
따라서 다이나믹 프로그레밍을 통해서 작은 문제로 쪼갠다. 즉 벨만 기대 방정식을 이용하여 주변의 가치함수와 한 타임 스텝만 고려하여 다음 가치함수를 계산하도록 작은 문제로 쪼갠다.
벨만 기대 방정식 수식은 $V_{\pi}(s)=E_{\pi}[R_{t+1}+\gamma V_{\pi}(S_{t+1})|S_{t}=s]$이고 계산 가능한 형태로 변경하면
$V_{k+1}(s)=\sum_{a\in A}^{}\pi(a|s)(r(s,a)+\gamma V_{k}(s'))$를 반복적으로 수행한다.
정책발전
정책발전은 널리 알려진 탐욕적 정책 발전을 사용하여 설명하면 어떤 행동이 좋은지 알 수 있는 큐함수를 이용하여 가장 큰 큐함수를 가지는 행동을 하면 수식 $\pi'(s,a)=\textrm{argmax}_{a\in A }q{*}(s,a)$ 을 통해 새로운 정책을 얻는다.
가치 이터레이션
최적의 정책을 가정하는 것은 처음의 가치함수가 최적이 아니라 틀린 가정이지만 다이나믹 프로그레밍을 이용하여 반복적 계산을 통해 최적 가치함수에 도달하고 최적정책을 구할 수 있다. 따라서 가치 이터레이션은 가치함수를 업데이트를 하면 자동적으로 정책도 발전한다.
벨만 기대방정식을 통해서 구하는 것은 현재 정책에 대한 참가치함수이다.
$V_{\pi}(s)=E_{\pi}[R_{t+1}+\gamma V_{\pi}(S_{t+1})|S_{t}=s]$
벨만 최적 방정싱를 통해 구하는 것은 최적 가치함수이다.
$V_{}=\underset{\pi}{\textrm{max}}E[R_{t+1}+\gamma V_{}(S_{t+1})|S_{t}=s, A_{t}=a]$
벨만 최적 방정식을 통해 문제를 푸는 가치 이터레이션은 시작부터 최적 정책이라고 가정하여 반복하면 최적 가치함수와 최적정책이 구해져 MDP가 풀리기 때문에 정책 발전이 필요없다.
벨만 최적 방정식을 계산 가능한 형태로 변환하면
$V_{k+1}(s)=\underset{\pi}{\textrm{max}}(r(s,a)+\gamma V_{k}(s'))$
정책 이터레이션과 차이점은 다음 상태를 다 고려하여 업데이트를 하는 것이 아니라 제일 높은 값으로 업데이트를 한다.
다이나믹 프로그램의 한계
1. 계산 복잡도
다이나믹 프로그램의 계산복잡도는 상태 크기에 3제곱에 비례하여 경우의 수가 많은 환경에서 사용하기 어렵다.
2. 차원의 저주
상태의 차원이 늘어나면 상태의 수가 지수적으로 증가하여 차원의 저주에 빠진다.
3. 환경에 대해 완벽한 정보가 필요하다.
환경을 포함되는 보상과 상태변환확률을 가정하여 풀었지만 실제 강화학습 문제에서는 이를 알 수 없다.
강화학습은 환경과의 상호작용을 통해서 입출력 사이의 관계를 학습하여 모델이 필요없다.
'AI > 강화학습' 카테고리의 다른 글
| 벨만 기대 방정식, 벨만 최적 방정식 (0) | 2022.04.25 |
|---|---|
| 가치함수와 큐함수 (0) | 2022.04.15 |
| MDP (0) | 2022.04.13 |